
最近突然为一个问题感到困惑不解,为什么算盘要分为上下两栏?梁上的每个珠子代表五,梁下的每个珠子代表一?为什么不是直接用十个珠子,每个珠子代表一?用十个珠子的话,可能准确点数珠子需要更加集中注意力(十个珠子要数清楚肯定比五个珠子费力),但珠算的规则可以大大的简化,几乎完全不用背诵“六上一去五进一”之类的口诀,只要会十以内的加减法就行了。而且,这样珠算的表现形式几乎就可以和纸上的形式一一对应,可以完全转移到纸上,可以和笔算互相印证。为什么不呢?
为了搞清楚这个问题,查找了一些资料,顺便发现中国古代不是只有毛笔,而是有很多硬笔的,比如石墨做的铅笔、和近代西方钢笔极为类似的竹制蘸水笔、还有鹅毛笔。“翰林”这个词大家都知道是很有学问的文化人,可大概很少人知道这个“翰”的意思就是羽毛笔。硬笔在制图、绘画等需要单纯线条的方面用的比较多,估计也会用于笔算。

1972年在甘肃武威张义堡遗址中发现的双瓣合尖竹管笔
经过搜寻,没有找到算盘问题的答案,却窥见了中国古代数学的发达强大。可惜,数学也像中国传统文化的许多其他方面一样,在满清入关之后日趋衰亡。我通过分析资料中举的例子,揣摩出了古代笔算一些基本用法,在此记下来免得以后忘了。 ^^
主要资料来源于这里,是个pdf。
记录数字的符号
实际上我认为汉字本身作为计数符号就相当好,笔画少,组合规则简单直观,有数位概念。欧洲语言中的数字太复杂冗长,以至于他们不得不借助于别的符号,甚至有的语言本身的数字表达法就是一团乱麻,比如法语,70说成60+10(Soixante-dix),71是60+11,以此类推79就是60+10+9。而80就是4×20(Quatre-vingts)。到了说99,那就要用得上三则运算了:4×20+10+9(Quatre-vingts-dixneuf)……
明朝数学家孙元化显然同意我的观点,比如他说三千六百九十三写成“三六九三”就行。
不过在之前的唐宋乃至更早的时期,人们一般不用汉字,而是用“数码”来记录数字。因为那时的计算工具主要是算筹,就是“运筹帷幄之中决胜千里之外”的那个算筹,也叫“算子”,《射雕》中的神算子瑛姑用的就是这个,用算筹摆出的数字就是“筹码”,其实就是一根一根的小竹签,摆在地上代表数字,把这种竹签的形状描到纸上,就是数码。一根就代表一,两根平行放就代表二,三根代表三,四根代表四,那么五用什么代表?两根交叉即可。六是上面一根,下面在垂直方向再放一根。七是上面一根,下面在垂直方向再放两根。八九以此类推。
那么似乎很明显,算盘的上下两栏、上栏数字代表五的做法是从算筹而来。不过算筹和算盘各自有不同的特点,一个数就平行放九根算筹,再连着排几个数,就几乎没法看清是几了,但算盘不一样啊。好吧,其实应该说,我知道算盘为什么会这样,我知道它的起源;但我想知道它为什么保持这样,没有变成别的样子,比如一列十个珠子。在我看来,数珠子的成本要远远少于在两套代表系统(一代表五和一代表一)之间切换和背诵超级复杂口诀的成本。
可以看出,数码有横式和竖式两套,写长数字的时候横竖交替使用,既美观又不容易与相邻的弄混。(比如把“朱月坡”看成“朱肚皮”……)
其实汉字的“一二三四五六七八九”也是从这些形状形变而来。不过汉字可以形变,算筹和数码却不能形变,于是就慢慢发展成两套系统了。
数码的写法,各个数学家可能有出入,不过总体是大同小异。
〇
中国数学中早就有“0”的概念,最初是用空一位来表示,至迟到宋代,已用圆圈“〇”来表示了。
正负数
正负数的概念也是一早就有了,一般用红色算筹代表正数,黑色算筹代表负数。写在纸上的数码,有的是直接在数字后面用汉字标明正负,有的是在负数上加一道斜划。
分数、小数
分数好写,就跟现在一样,中间划道线,上面写分子,下面写分母。
小数的处理各家有所不同,一般是个位数对准,有的在个位数下面加注单位。
一元高次方程
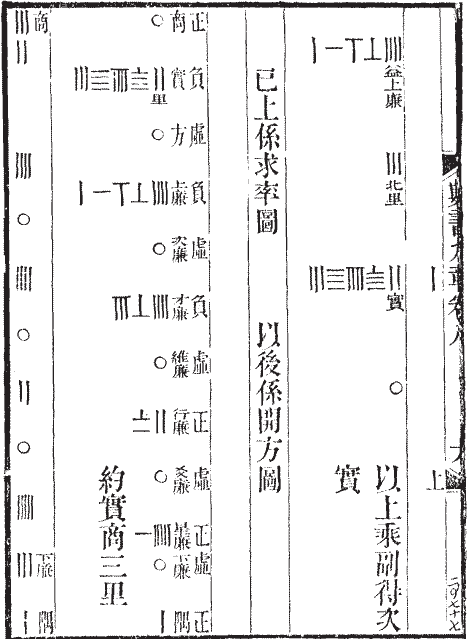
上图是南宋大数学家秦九韶所著《数书九章》中的“遥渡圆城”题中的算式(据“宜稼堂丛书”本),左边的部分相当于这样一个方程式:
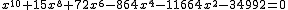
可以看出,中国传统数学的写法相当于把现代的方程式逆时针旋转了90度,最上方写常数项,然后从上往下依次从低次项写到高次项。旁边有汉字附注,“正”“负”表明正负数,“里”是单位(因为这是应用题),“实”表示常数项,“方”表示一次项的系数,“隅”表示最高次项的系数,“星廉”“行廉”等是各项的系数,可以想见,中国古代数学家给各次方都起了一个独特的名字。为0的项既用了“〇”,又在后面注明了“虚”。这题的答案是三。
矩阵
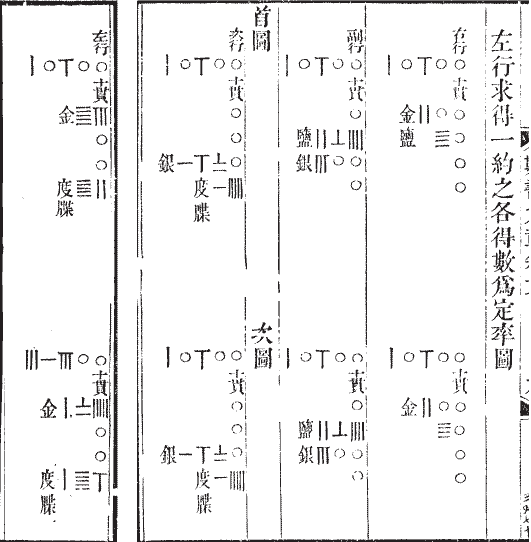
上图是《数书九章》中的“均货推本”题中的“首图”与“次图”(据“宜稼堂丛书”本),它的上半部分相当于这样一个矩阵:
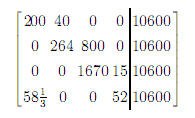
依旧,常数项写在最上面,其他各项从上往下依次写。这里的“五”是用五个平行笔划表示。然而,我没看出“五十八又三分之一”的三分之一是怎么表示的,也许是有个我不懂的特殊标记?但此图的下半部分明显是对上半部分的变换,含有“五十八又三分之一”的那一列的每个系数都被乘以三,把分数转化成了整数,因此就变成了[175 0 0 156 | 31800],所以上面那个数必须是“五十八又三分之一”。
此例可以明显看出“〇”的使用非常成熟。
欧洲的笔算
欧洲的加减号出现于15世纪,乘除号出现于17世纪,等号发明于1557年,正负号的使用也在17世纪,小数点由Napier(1550-1617)发明。17世纪之后,欧洲的笔算才由早期逐渐进入近代。
明代
明代筹算已经逐渐退出历史舞台,数学家直接用笔算,民间则是珠算大行其道。虽然当时欧洲的笔算整体上不如中国先进,没有负数符号,小数记法极为繁琐,但明朝仍然翻译出版了一些关于西方数学的书籍,数学家孙元化、梅文鼎等都比较了中西演算,推崇西法的一些优点,将之与中国传统演算法相结合。此时的中国并不固步自封,而是提倡学术交往、关注世界潮流,西方有了新的进展,在中国也会很快有翻译、介绍。
清代
中国人已经根本不知道筹算为何物,连国家钦天监的天算家都不知道,当他们在朝鲜见到算筹时感到万分惊奇,其震惊大概不下于在朝鲜见到翻版华夏衣冠吧。笔算基本陷于停滞状态,直到清末西方新式笔算再次传入中国,1900年左右开始使用印度-阿拉伯数字,中国传统笔算完全被西方笔算系统所取代。
逆水行舟,不进则退。当中国停滞的时候,别人却在一日千里的发展。先进很快就变成了落后。三百年的时间让中国陷入了深渊,不知道是否也需要三百年来挽回。
文中可能有错漏之处,欢迎指正。
本文作者:Betty | 本文地址: https://myfairland.net/chinese-traditional-calculation/
本站文章除特殊标明者外均为原创,版权所有,如需转载,请以超链接形式注明作者和原始出处及本声明

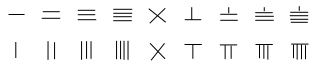


第一次知道原来还有双瓣合尖竹管笔
真的是开眼界了。
韩侑的最近博客文章没完没了的结婚进行曲
看历史总是一件很悲的事情…
Donald的最近博客文章COMODO Internet Security FAQ(3) CIS常见问题(3)Defence+部分
真是没想到
我们现在从学校到单位全都用计算器了。。。。。
想当初 古希腊文化 也是在希腊绝种了,又从欧洲传回去的
是阿拉伯人帮忙保存,传回去的,那时阿拉伯是先进文明的种族
可是现在阿拉伯却成了愚昧落后的象征……
受教育了。
It’s been made from durable cedar wood that promote <a href="http://www.beatsbydre99.com ">beats by dre</a> rustic finish. On top of that,For very long years, probably the most popular kinds of exterior shutters continues to be referred to as cedar board and batten shutters, it is <a href="http://www.discountmonclers.com ">moncler jackets</a> less costly compared with other kinds of shades.