关于维度,看过一些书,也经常想这个问题。最近有些新想法,说出来跟大家探讨一下。只是一些想法,一些猜测,一些可能性的探讨,不一定对,但也许有些地方蒙中了真相,谁知道呢。
在爱因斯坦的体系中,我们所处的空间是三维的,加上时间一共是四维。但是时间这个维度是很奇怪的,性质跟其他三个维度完全不一样。
空间的三个维度,长、宽、高这三条轴,是两两互相垂直的,长度的轴和宽度的轴垂直,高度的轴和长度的轴垂直,高度的轴和宽度的轴也垂直。这就是现实空间的所有三个维度,我们在现实世界中,再也无法想象出另一条轴能和这三条轴都垂直。
在数学上,构造高维空间是很容易的,可以轻易地增加一个轴,让它和原有的轴全部垂直。虽然我们想象不出来实际的样子,但是不需要想象出来,只要这些轴满足垂直的定义和性质,就可以计算各种数值了。比如什么“两个平面相互垂直当且仅当它们的法向量相互垂直。一个更几何的方法是看两个平面的交线(如果没有说明两平面平行)。选择一个平面,过两平面交线上的一点作一条垂直于交线并在平面中的直线,如果这条直线与另一个平面垂直,那么两平面垂直。” ((http://zh.wikipedia.org/wiki/%E5%9E%82%E7%9B%B4)) 现在流行的弦论轻易地搞出了 10 个维来解释我们的世界,还有 11 维和 26 维等等说法。
然而,时间,跟长宽高这三维、跟数学上的维度,看起来完全不一样。时间似乎显然并不垂直于长宽高这三维。而且,时间还有非常奇特的性质,比如,它是有方向性的,我们只能感觉到时间的流逝,无法逆转,无法同时感受两个或多个时间点。
我的新想法是,也许,时间本身其实是跟其他维度一样的普通维度,就像数学上定义的,跟其他维度互相垂直,我们的感受不同是因为我们处于三维世界,只能以这种特殊的方式感受它。各个时间点的内容(所有物体的位置、状态等等)是一直都存在着的,只不过我们一次只能感受到一个时间点而已。在三维世界中只能实在地感受三维事物,更高的另一个维度只能以这种特殊方式感受,而我们恰巧把这另一个维度称为时间。
拿低维世界来打比方也许比较容易理解。比如说,这儿有一个三维的球体。假如有一群人生活在二维国所在的世界,他们只能感受到平面上的东西。对于球体,二维世界的人只能感受到球体与他们所在的平面相交形成的切面,也就是一个圆,他们是感受不到高度的。
那么,现在这个球体开始往下动。在三维世界中,物体可以上下移动。结果是球体和那个平面的切面面积变化了。但是二维国的人感受不到高度,他们没有高度上的上下移动这么一个概念。在他们看来,只是这个圆变大或变小了。球体一直往下移动到只有顶端接触那个平面,在二维国的人看来,就是这个圆一直变小,直到变成一个点。
在我们三维世界看来,这个球体的各个切面是同时存在的。但是二维国的人一次只能感觉到一个切面,他们能感觉到这个切面的变化,或者说流逝,但不可能同时感受到多个切面。有点像我们世界中的时间,对不对?
也许我们的世界也是,各个时间点的内容是一直都存在着的。现在的我,上一秒的我,昨天的我,明天的我,同时存在着(“同时”这个词在这个语境下不是很合适,希望你们懂我的意思,我是说所有不同时间的我都一直存在着,不是这一瞬间存在,下一瞬间消失)。
你或许要问,如果昨天的我和现在的我同时存在,而且坐在同一个房间同一个地方,那不是重叠了吗?一个昨天的我怎么可能重叠压在现在的我身上?回答是,就是重叠了。重叠在另一个维度上。就像球体,横切面有无数个的圆,我们知道这些圆都处于不同的高度上,但是二维国的人没有高度的概念,一次只能感受到一个圆,如果告诉他们这些圆同时存在,他们只能认为这些圆是重叠着的。
再打一个比方也许更好理解,就像电影胶卷,一部电影由许多帧组成,一帧是一个时间点。每一帧的画面实际是二维的,你如果能把它想象成三维的更好,不行的话也没关系。把这些帧连续播放,我们能看到电影中的人在动,事情在发生,换句话说,时间在流逝。
如果我们把胶卷一帧一帧的摞在一起呢?从一帧到另一帧的转变仍然叫做时间,而这时间与帧所在的平面之间的关系,变得垂直了。
我们能看到这些帧摞在一起,而且我们看到,这些帧是同时存在的。假如电影中有一个人长大了,我们看到有一帧是他小时候的状态,有一帧是他长大后的状态(当然可能还有许多帧是中间状态)。而电影中的人,假如他们有感受的话,他们一次只能感受一帧的状态,到下一帧,他们的感受就是时间流逝了,他们无法想象这些帧能同时存在。
我们的世界就像电影胶卷,每一个时间点是一帧,只不过我们的帧是三维的。并且,因为我们自己处于三维世界,我们看不到这些帧摞在一起,我们只能一次感受一帧,以时间流逝的方式感受这些帧。只有比我们更高维度的世界才能看到这些帧摞在一起。
用这种理论,时间旅行的各种悖论就变得很好解决了。一个人回到过去杀死外祖父,他的妈妈还会不会出生,他自己会不会存在?会,完全不受影响。你把球体砍成两半,其中一半扔掉,另一半还在,完全不受影响。你把电影胶卷剪了,把故事前半截的胶卷扔了,后面的故事仍然还在,完全不受影响。所有的帧是同时存在的,一直存在的,后面的帧的存在并不依赖于前面的帧。
时间旅行的另一个经典问题,一个人回到过去,比如说去年,那么去年的他是突然消失了?还是两个他同时存在,一个年轻些,一个老一些?回答是同时存在。就像你把电影后半截的主角从胶卷上抠下来,粘到前半截的胶卷上,这时前半截的胶卷上就同时存在两个主角了。但是注意,后半截的主角抠下来了,后半截的主角就没了,当电影放到这里的时候,前半截的主角会突然消失。一个人穿越回去年,现在的他和去年的他会同时存在,但一年后,去年的他不会变老变成另一个现在的他,而是突然消失了。现在的他能存在多久,视乎你抠了多少胶卷上的主角。比如你把第 60-70 分钟的主角抠出来,粘到第 50-60 分钟的胶卷上,那么,第 50 分钟时就会存在两个主角,一个老一些,一个年轻一些,10 分钟后,两个主角都突然消失了。第 80 分钟,主角又出现了。假如你不是粘到第 50-60 分钟的胶卷上,而是粘到第 40-50 分钟的胶卷上,那么,第 40 分钟时会出现两个主角,第 50 分钟时老一点的主角消失了,年轻一点的主角还在,第 60 分钟时,年轻一点的主角也消失了,第 80 分钟,老一点的主角又出现了。
也许你会问,这样事情不就不连续了吗?人怎么能突然消失突然出现?回答是,连续只是我们在三维世界中感受世界的常规方式,更高维度下的运动,低维度下看来很可能就是不连续的。比如一个球体在二维国运动,在一个位置往下运动,直到离开二维国所在的平面,然后横向运动一段距离,再往上穿过二维国所在的平面。在三维世界看来,它的运动一直是连续的。但是在二维国看来,情况是一个圆逐渐变小,变成一个点,然后消失了,过了一会,突然在另一个地方出现一个点,然后慢慢变大变成一个圆。如果我们掌握了时间旅行技术,多半我们已经掌握了如何利用更高维度运动,而这在三维世界看来就是不合理,无法解释,违反因果律的。
另外请留意一点,当一个人时间旅行的时候,不是说只要他回到过去,老一秒的他、老一天的他、老一年的他,他所有剩下的生命,都自动跟着他一起回到过去了。就像把第 60 分 01 秒的主角抠出来, 60 分 02 秒、60 分 03 秒等等的主角不会自动也跟着出来。你抠多少帧就有多少帧。只抠一帧的主角粘到前面胶卷上,那就相当于主角只回到过去了一瞬间。所以,时间旅行的时候,不仅要设定你想回到什么时候,而且还要设定你想带走多长的时间。这种设定,我在科幻作品中似乎还没看到过(如果你看到过,请指教)。
只有你设定的这个时间长度是回到过去的,剩下的时间还是按照原来的节奏。也就是说,你一共还是只能活那么多年,只有那么多时间,时间旅行不能让你变得长命,只不过能让你以不同的方式分配时间。
同时,也许更重要的是,你回到过去,所做的事不能改变现在,不能改变未来。也不存在平行世界、多个时间线。第 60 分钟的主角带走 10 分钟的时间,回到第 50 分钟,不管他做什么事,第 70 分钟一到,出现的还是原来那个第 70 分钟的他,发生着原来第 70 分钟的事。第 50 分钟的女主角原本不爱他,他回到第 50 分钟让女主角爱上了他,可是第 70 分钟一到,世界还是女主角不爱他的那个世界。所有的帧早就一直存在,你改变这一个帧,不会影响到其他帧。涉及到高维世界,三维世界的因果律就不管用了。
这样说也许有点悲观消极,显得有点宿命论。似乎一切早已命中注定,又何必去争取?但是,我们感受不到的东西,对我们来说实质上就相当于不存在。也许对于高维世界的生物来说,看我们的生命就像看电影,一切早已注定好了。但是我们自己是不知道的。就像电影中的人,自己的命运自己是不知道的。不管多么颠沛流离、曲折离奇,电影中的人物总是奋力去争取去追求。因为我们看到的是,去追求,才能和自己的目标更接近。
高维世界的生物对我们来说,可说是真正的神吧。在高维空间,他们不但能看到我们生命电影的所有帧,看到我们的过去和未来,而且,他们说不定还能拿剪刀,把我们从胶卷上抠下来,粘到别的胶卷上。
本文作者:Betty | 本文地址: https://myfairland.net/dimensions-and-time-travel/
本站文章除特殊标明者外均为原创,版权所有,如需转载,请以超链接形式注明作者和原始出处及本声明
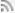
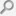



我去 太抽了 完全看不懂
确实是很新颖的想法,不知道是不是作者原创,通篇读下来很是佩服,同意绝大多数的观点和看法,希望能就此问题多交流。
嗯,是我自己想的,当然肯定也是看了许多书受了启发的 :)
时间这个维度,就拿太阳和地球来说,地球上所知的太阳是8分钟之前的。
这个 8 分多钟是因为从太阳到地球的距离,以光速运动的话需要 8 分多钟的时间……地球上看到的阳光是 8 分多钟以前的,如果太阳突然消失,地球上的阳光在 8 分多钟后才会消失。包括引力也是以光速运动的,所以如果太阳突然消失,太阳的引力也会在 8 分多钟后才消失,地球还是会围绕着太阳曾经所在的那个点转一会呢~
嗯 我是来点赞的
第一次看到有人把维度描述的如此浅显易懂。
我还担心写得没人能看懂呢,你让我好感动~ :)
我也看懂了。好骄傲
低维度的人不知道自己剩多少时间,时间旅行的时候怎决定抠多少呢?
为什么要知道还剩多少时间呢,我觉得一般也不会非要把剩下的寿命都用上吧……非要用的话就抠到抠不动为止,汗……而且能时间旅行了,应该就能知道这些了吧……还有需要的能量应该是跟抠的时间长短成正比的吧,一般人估计也抠不起太多……
二维国的世界就是三维世界去掉任意一维嘛,二维世界还是有时间维度的,干嘛不去掉时间维…拿三维世界的感受来假想二维世界,又假想它们之间的关系来推测四维世界,最后又想用四维世界的手段来改变三维世界,有点想不通
并不是说先有一个时间维,二维世界要保留它,而是二维世界只能实在地感受两个维度,对于两个维度之外的维度,只能用特殊的方式感受。即使去掉时间维,保留长宽高三个维度,也是一样的,二维世界只能实在地感受两个维度。多出来的那个维度,不管是长、宽还是高,二维世界无法把它感受为长、宽、高,只能以特殊的方式感受,比如流逝的方式。你可以把这个多出来的维度叫做时间,但即使叫做别的名字也是一样。再想想那个电影胶卷的比喻。
春晓的自媒体里推荐的这篇文章、看完了、讲得很通俗易懂啦
第一次见有人把维度、时间旅行讲得这么深入浅出、接地气!人工点赞!
这……宿命论啊。感觉文中用可剪裁的实物(球,电影胶片)类比“时间维度“的做法是不妥当的。要想象出“剪裁时间”的具体形象,除非我们能够想象剪裁空间本身,使之发生扭曲、重叠(类似“曲速引擎”)。不过,扭曲空间也必然同时影响到时间这个维度。所以楼主这个推论所立足的实体模型——电影胶片,其实是无法代表“时间维度”性质的。另外,关于文中体现出的决定论,宿命论观点,也无法令人赞同。楼主在不妥当的类比下,将时间想象成一个既有的“存在”,这其实符合我们对“空间”的感受。欧式几何告诉我们,空间就是一种既有存在,一条直线可以无限延伸。然而,这是事实吗?现代物理学说,不,时间与空间均无法脱离物质而存在,他们是伴生的。所以,假定时间是一种既有存在的宿命论,并无依据。
请看本文的第一段和倒数第二段
看完感觉和双鱼玉佩很像